/首页
/开源
/关于
数据结构之树的基本枯燥概念(一)
发表@2018-09-13 09:15:22
更新@2023-01-21 22:47:40
树,大概如下图所示:  你要知道,升级到了一所高级中学,那学习的内容自然也要是升级的,不能一辈子都抱着线性表出去装X,被反杀的概率很高的。 新的学校,新的老师,新的内容。什么?记忆力不好?学习树这种高危的数据结构,记忆力不好迟早要玩完。别人搞出来的程序都是O(nLogn)就搞定了,怎么到你这里全是O(n^n)?  篇幅和深度的问题,只讲二叉树,至于三叉树、四叉树、五叉树,是以后的事情了,因为说起来二叉树是计算机软件中应用的相对广泛的。顾名思义,二叉树就是一个树干只能少于两个叉,绝对不能滋出来第三个叉。用抽象思维抽一下,就能抽出如下数据结构: 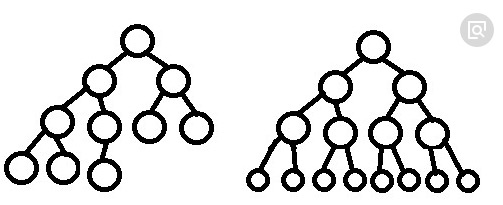 上图中可以看到,有些圆圈上只有一个叉,末枝的圆圈则是一个叉都没有,但是,绝对不会产生一个圆圈具备三个以及多余三个的叉。 为了避免有人开小差,先在这里说下树这种数据结构在菜逼phper能接触到的软件体系中起到了什么作用。想了想,当然是mysql了(*多说两句昂,这年月,但凡是个公司,哪怕只有3个人也得问你如何实现高并发、如何优化mysql数据库,即传说中的“面试造火箭,入职拧螺丝”。实际上,问问这些问题也未尝不可。一般说来,通过这些问题可以摸清楚一个phper门脉咋样,至于你能不能答出来可能并不会影响应聘结果,只不过是如果你答得不错,对于面试者而言可能是锦上添花*)。天天有面试官问你mysql索引如何优化,而你也就是靠着网上复制粘贴的那些个博客上记录的文字在做记忆和背诵。然而,如果你搞明白树,那你一定也能够从根本上理解索引为什么要如此优化,因为索引用数据结构就是树。 前面说了,记忆力不好的迟早要倒霉的。  我们将图三中的圆圈叫做树的“结点”,结点的子树的总数叫做结点的“度”。图三中,最下面一层没有任何子树的结点,我们称之为“叶结点”,叶结点的度统统为0。而度不为0的结点则被称为非终端结点或分支结点,除了跟结点外,这些分支结点又可以叫做内部结点。结点的度的最大值就是整个树的度!而树从跟结点开始一直到最下面一层,历经的结点的层次就叫做树的深度。画个图意思一下:  可以看到,根节点A有两颗子树:B和C,所以根节点的度为2。其中B有三个子树,所以B结点的度为3,是整个树中最大的,所以树的度就为3。而D、E、F、H由于没有任何子树,所以称之为叶子结点。根节点占据树的第一层,依次为基准往下数一直到H结点,一共四层,所以数的深度就是4。以上这些就是树中常遇到的一些基本概念,记你是需要记住了。有些是你上学那会儿就偷懒没记的,现在,也该还了吧? 除此之外,还应该注意到,A是B和C的父节点,B和C则分别是A的左子树和右子树,而B和C之间以兄弟相称。 其实,作为二叉树,自然拥有一些普通的屌丝树无法拥有的特性,说到这里,难免又是一波儿背诵: - 二叉树每个结点最多拥有两颗子树,也就是结点的度最大为2 - 二叉树结点的左子树和右子树是有顺序的,而且次序不可以颠倒。所以当二叉树中结点有一颗子树,那也得搞明白到底是左子树还是右子树。 二叉树算是普通屌丝树中的高配版本,但是,从二叉树中依然也有“高配”和“屌丝”两个版本。下面是一些高配版本的二叉树,你们感受一下: 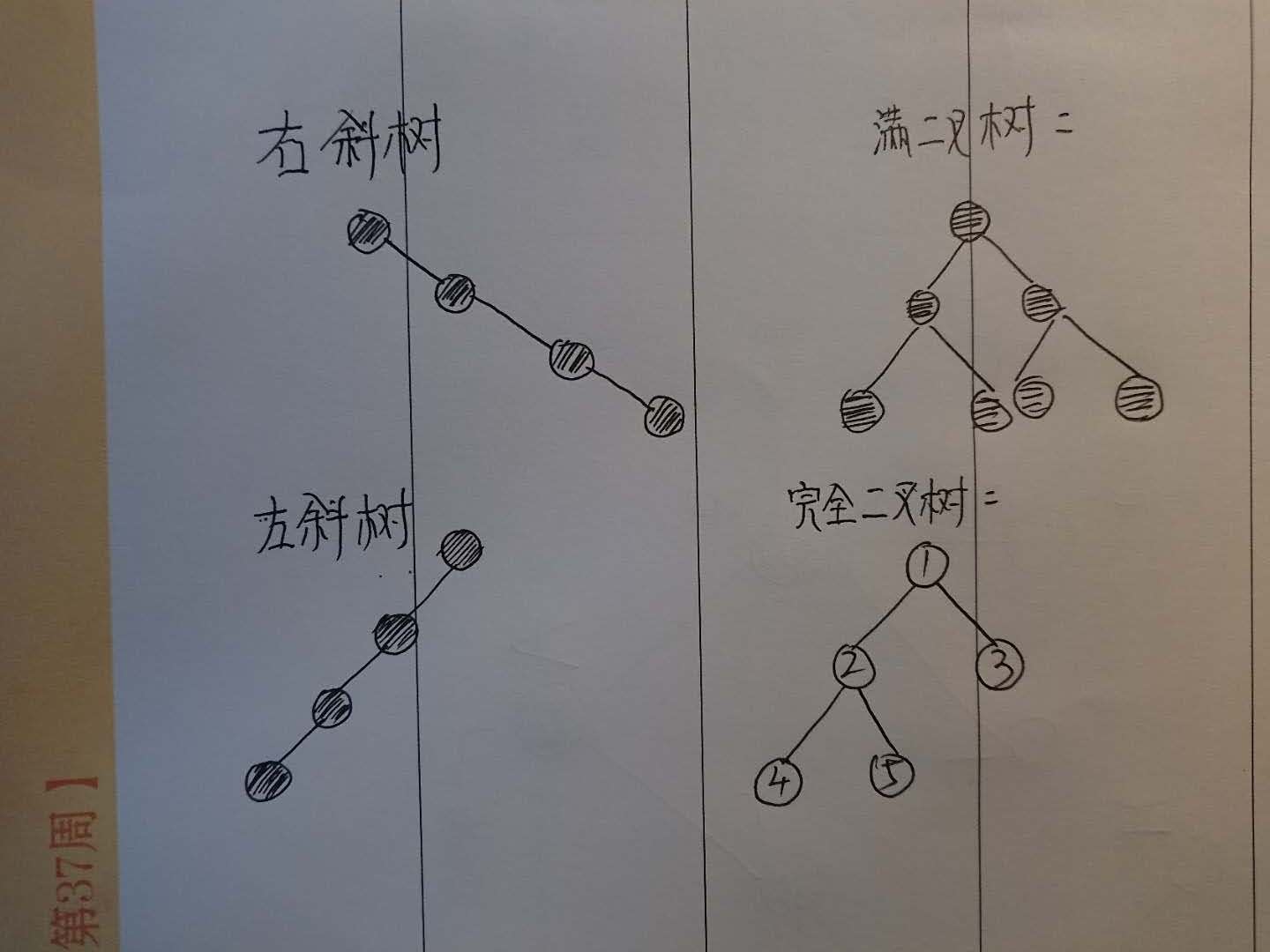 斜树是一种比较偏执的树,总体来说,他是一斜到底的。前面说了,二叉树的子树是有顺序的,左子树就是左子树,右子树就是右子树,二者不可混淆。所以,斜树也是一样的,向左边一斜到底的叫做左斜树,向右边一斜到底的叫做右斜树。这个时候树,是不是看起来有点儿像线性表?啊哈哈。 满二叉树是比较容易理解的,这东西以垂直中轴线为中心的话,左右是对称的。从定义上讲满二叉树所有结点都存在左子树和右子树并且所有叶子结点在同一个深度的层上。 最后一个叫做完全二叉树的,比较膈应人,因为“完全”和“满”乍一听总有一种近义词的感觉。对于完全二叉树,我们首先为树中的每个结点从根节点开始从左往右、从上至下开始编号,如上图中所示。如果说结点没有出现空缺断档,而是一直连续的,那么就称之为完全二叉树。满二叉树一定是完全二叉树,反过来就不能成立了。向下面这种树,就不是完全二叉树: 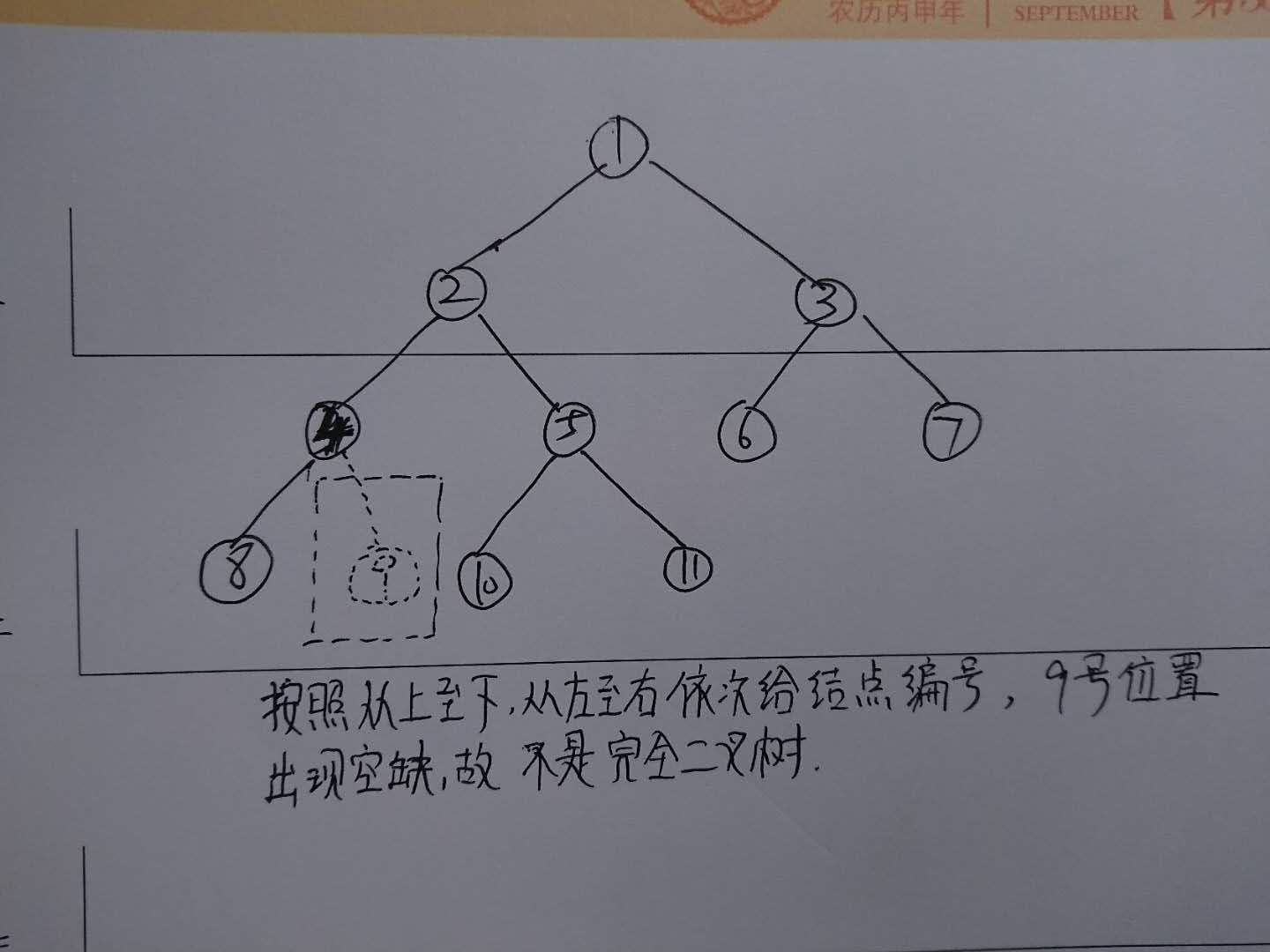 二叉树有一些数学特征,我列(zhan)举(tie)出来,大家感受一下,最好能够像我一样熟(chui)练(niu)记忆于心中: - 二叉树在第X层上最多拥有2^( X - 1 )个结点 - 深度为X的二叉树,最多拥有2^X - 1个结点 - 一个拥有N个结点的完全二叉树(注意是完全二叉树),其深度为floor( log2N + 1 )。floor就是php中floor函数的意思。 - 任意一个二叉树,如果叶子结点数量为X,度为2的结点数量为Y,那么一定有X = Y + 1 前面说过了,线性表的存储结构可以采取顺序存储方式和链式存储方式两种方案,同样,二叉树也一样。但是,通过上面的介绍可以感受到,二叉树是一种典型的一对多的逻辑结构,使用顺序存储并不合适,所以一般我们自己不作死的话,采用链式存储方式总是没有错的。 啦啦啦,作为一个比较新的、相对来说记忆内容较多的、相对比较枯燥的新概念来说,就先到这里吧,如果还要接着往下直接贴代码,至于你能不能受得了,反正我受不了。 